Programming Projects
Networking - client/server ddos simulator
Github link
This was a project for CNT 4504 - Computer Networks. That course focused on architectures, protocols, and layers in computer networks and develop client-server applications. Topics include the OSI and TCP/IP models, transmission fundamentals, flow and error control, switching and routing, network and transport layer protocols, local and wide-area networks, wireless networks, client-server models, and network security.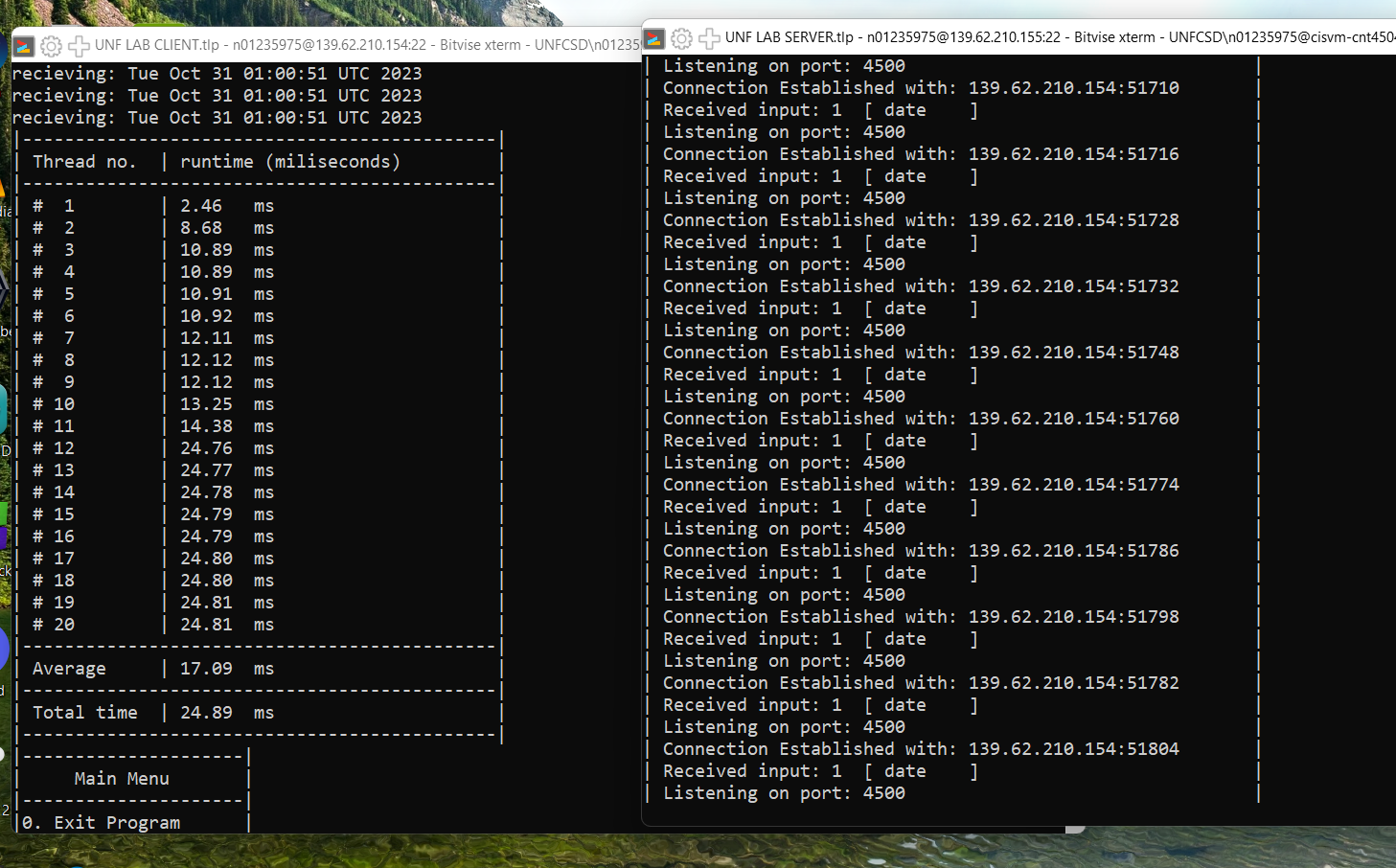
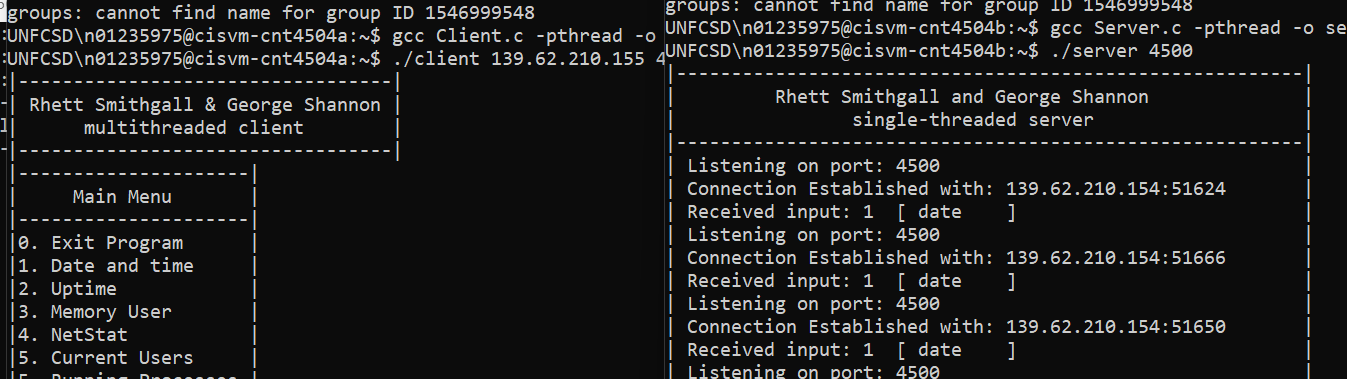
In this project I created a multi-threaded server/client pair in C. The client sends requests to server for common linux commands like date or netstat and the server returns the result of those commands. Each thread from the client is timed, and the total time of a batch of requests is recorded. Using this tool you can clearly see how response time is impacted when a system is overloaded with requests. For example, you could run a large batch, say 1000 date requests, and see the slow slope in times. The first few will finish quickly but then as the server runs out of proccesses the threads will slow down, then speed up again as requests are proccessed.
Math Monster
Github link
Video feature
Math monster is a calculator made from an antlr-based compiler. You put in math and it correctly follows the order of operations to give you the correct solution. As you can see below it can handle some pretty complicated expressions including square roots with different bases, trigonometric functions, exponents and constants like pi and Eulers number.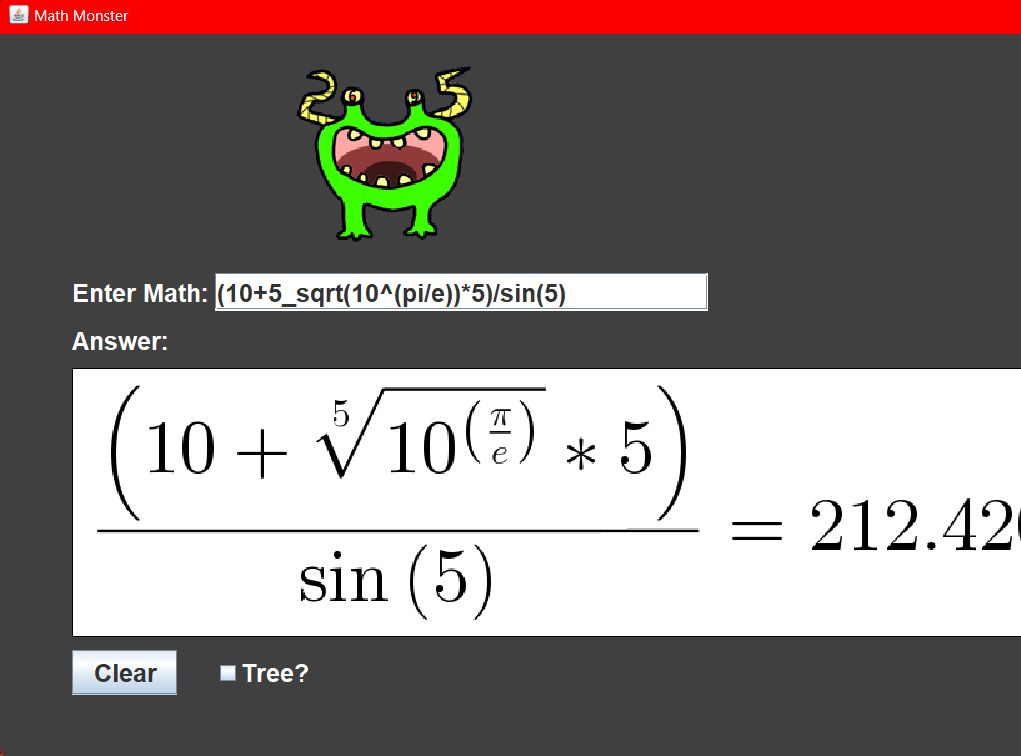
Why did I make this?
many modern online calculators like desmos, mathway, and wolfram alpha are capable of some very complicated order of operations. It doesn't matter how many overlapping parentheses,functions and operators you have, these calculators are capable of giving the correct answer every single time. In order to figure out how these modern calculators work I made my own; "Math Monster"How did I make this?
A naive approach
From the outside these calculators might seem simple, perhaps one could be made using regular expressions and typical programming tools like conditional statments. You would quickly find however, that while you could easily make an arithmetic calculator when you get into more complicated expressions with parentheses and divisors and square roots the overlapping nature of these make it very difficult for regular expressions to parse every possible entry. for this problem a more comprehensive solution is required.Compilers
Compilers are known even to novice programmers for taking a massive input (code) and parsing it into assembly or bytecode. Important for this application, the principles of compiler construction can be used for making a calculator. For this project I used a public Java compiler standard known as antlr. While antlr handles most of the structure of the compiler the critical features like the lexer, grammar and code generation must be provided by me. Compilers are broken into 3 primary parts, the lexer, the parser, and code generation. In the following sections I will explain what math monster does at each section.Lexer
Here the inital input is broken down and each piece is assigned a label also called a token. This part can also be called tokenization. a number like one is labeled a number, an operator like + is labeled an addop and functions like sin are labeled trigop. Every single piece gets a label.
parser
next the parser moves through the tokens from the lexer and searches for patterns. It will only search for a single pattern at a time, so by setting these in a specific order youc can enforce the order of operations. In the case of math monster it first looks for parentheses, then exponents, then trigops, then mul/divops, and finally add/subops. When it find a match it will make the parts into a node, the parts into leaves, and rename the group to match a new token. NUMBER ADDOP NUMBER becomes ADDOPGRP for example. At the end of the proccess the parser generates a tree of all the nodes. First it finds all multiplication group patterns, because multiplication comes first in the order of operations
next it turns this group into a small tree

this proccess repeats until each part of the expression is in the same larger tree

Parse tree walker and dijkstra's shunting yard algorithm
This is the largest and most complicated part of the program, the parse tree walker. The walker works by navigating the tree with a depth-first search. In a depth-first search you start with the left most child of each node and traverse until there are no more left children, then you search for other nodes on the same tier until you find one with more children. The walker only takes action when leaving a node, this is why in the animation below the program seemingly ignores the first few nodes in green. It isn't until the walker reaches one of the bottom leaves and is forced to return to a higher tier node that it executes some code associated with that node. Every node has a special action associated with it based on it's token. Numbers for example are simply added to the stack. More complicated nodes like addopgrps will pop 2 numbers from the stack, add them together, and push the result back into the stack.
This method of using a stack to evaluated expressions is derieved from dijkstra's shunting yard algorithm. the shunting yard algorithm is a method for parsing arithmetical or logical expressions, or a combination of both, specified in infix notation. It can produce either a postfix notation string, also known as reverse Polish notation (RPN), or an abstract syntax tree (AST). The algorithm was invented by Edsger Dijkstra, first published in November 1961, and named the "shunting yard" algorithm because its operation resembles that of a railroad shunting yard.
